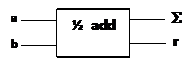Oro BIANCO

Menu

Accueil

Lycée
Terminale
Spécialité
Première
Seconde
MPI

Collège
Troisième
Quatrième
Cinquième

Et Plus
Rando

Privé

 
Télécharger :pdf

 

MPI n°15 : L’additionneur binaire

 

Objectif : Réaliser un additionneur binaire à l’aide de portes logiques.

 

On se propose d’étudier un montage à portes logiques réalisant l’addition de deux nombres binaires, le résultat étant donné en binaire.  Exemple : en décimal, l’addition 2 + 3 = 5.

Notre montage doit être capable d’effectuer la même opération en binaire, c'est-à-dire :  10 + 11 = 101.

Ce montage appelé additionneur binaire ou encore additionneur logique est une application des portes logiques.

 

I.       Le demi–additionneur

 

C’est un montage réalisant l’addition de 2 nombres binaires de 1 bit chacun, donc l’addition de deux bits.

 

1.      Table de vérité du demi–additionneur

 

a et b sont deux chiffres binaires (bits) ; on appelle :

  • S (sigma) : la somme de a et de b
  • r : la retenue de cette somme

r

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

a

 

 

 

0

 

 

 

0

 

 

 

1

 

 

 

1

+

b

 

 

+

0

 

 

+

1

 

 

+

0

 

 

+

0

r

S

 

 

 

0

 

 

 

1

 

 

 

1

 

 

1

0

 

Le résultat de l’addition est le nombre binaire  r S.

Il y a une retenue lorsqu'on réalise l'addition : 1 + 1 ;  en effet 1 + 1 = 2 en base 10 soit  1  0 en base 2 : on pose 0 et on retient 1 dans ce cas.

 

è En déduire la table de vérité du demi–additionneur :

 

a

b

r

S

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

On reconnaît les tables de vérité de 2 fonctions logiques :

Pour la somme S, c'est la fonction : . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Pour la retenue r, c'est la fonction : . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 

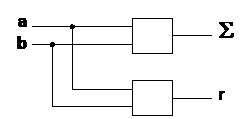
2.      Le circuit élémentaire (demi–additionneur)

En utilisant les résultats précédents, compléter le schéma du demi–additionneur :

 

1

II.   L’Additionneur complet

 

C’est un montage réalisant l’addition de 2 nombres binaires de plusieurs bits chacun.

 

1.      L’addition de 2 nombres de 2 bits

 

Soient A = a2 a1 et B = b2 b1 les deux nombres binaires à additionner :

 

r2

r1

 

 

 

Exemple :

1

 

 

Ce qui équivaut à :

 

 

 

a2

a1

 

 

 

1

0

 

2

+

b2

b1

 

 

+

1

1

+

3

r2

S2

S1

 

 

1

0

1

 

5

 

Le résultat de l’addition est le nombre binaire  r2 S2 S1.

 

2.      Schéma de l’additionneur de 2 nombres de 2 bits

 

La somme S1 et la retenue r1 sont issues d’un demi-additionneur.

S2 dépend de la retenue précédente, donc de r1.

r2 est la retenue de la somme S2.

 

Donc, en plus du premier demi-additionneur relatif à S1, le montage nécessite deux demi-additionneurs et un porte OU, soit au total 3 demi-additionneurs et 1 porte OU pour un additionneur complet 2 bits.

 

è Réaliser le circuit logique de l’additionneur complet de 2 nombres de 2 bits représenté ci-contre :

è Réaliser les additions : 10 + 10 ; 11 + 11

è  Vérifier en posant l’addition.

2

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 

Remarque :

Un demi-additionneur :

 

Peut se représenter par :

3

à

4

 

Cela permet de simplifier les schémas des additionneurs binaires. Représenter ci-dessous le schéma simplifié de l’additionneur 2 bits.

 

 

 

III.           Additionneur complet de 2 nombres de 3 bits et 4 bits          

1.      Additionneur complet de 2 nombres de 3 bits

 

  • Dessiner le schéma du circuit réalisant l’addition de A = a3 a2 a1 et de B = b3 b2 b1.
  • Réaliser le circuit pour effectuer les additions suivantes : 100 + 110 ; 111 + 111 ; 101 + 110 ; 101 + 011.
  • Vérifier le résultat donné par le circuit en posant l’addition.

 

 

 

2.      Additionneur complet de 2 nombres de 4 bits

 

  • Dessiner le schéma du circuit réalisant l’addition de A = a4 a3 a2 a1 et de B = b4 b3 b2 b1.
  • Réaliser le circuit pour effectuer les additions suivantes : 1010 + 1110 ; 1011 + 1011 ; 1001 + 1111 ; 0011 + 1011.
  • Vérifier le résultat donné par le circuit en posant l’addition.