<<<<<< Retour

Télécharger :

 

TP de physique n°7 : Relativité du mouvement

 

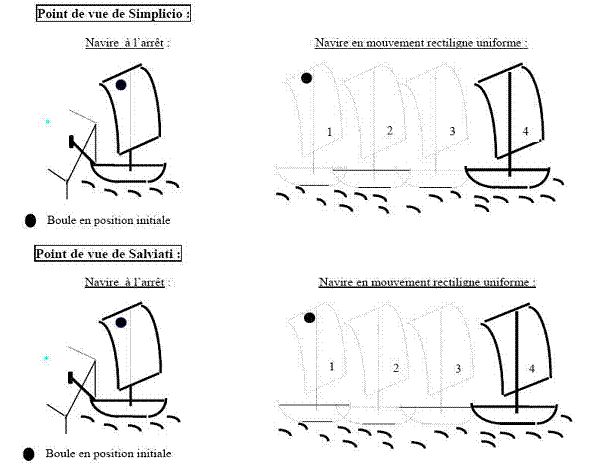
I.       QUESTION PRELIMINAIRE : le mouvement d’un objet dépend t-il du référentiel que l’on choisit ?

1.      Extrait du «Dialogue sur les deux plus grands systèmes du Monde» Galiléo Galiléi (1632- Editions du Seuil 1992)

Dès le début du XVIIe siècle, Galiléo Galiléi est convaincu par le modèle héliocentrique du monde (la Terre tourne autour du soleil). L’un des arguments principaux des détracteurs de Galilée consiste à affirmer que nous devrions nous rendre compte d’un mouvement éventuel de la Terre. Par l’intermédiaire du dialogue entre les deux personnages fictifs- Simplicio et Salviati, Galilée essaie de réfuter cet argument.

Rem : On suppose les frottements négligeables et on considère le navire en mouvement rectiligne uniforme.

 

2.      Exploitation

Q1. Simplicio parle d’un «mouvement naturel de la boule» de quel mouvement s’agit-il (c’est le même que celui du parachutiste lorsqu’il n’a pas encore ouvert son parachute) ?

Q2. Avec le point de vue de Simplicio, puis le point de vue de Salviati, représenter sur les schémas ci-dessous quelques positions de la boule de plomb lorsque le bateau est au repos ou en mouvement rectiligne uniforme.

II.   ETUDE EXPERIMENTALE

1.      Problème

On se propose de faire l’expérience – comme le demande Salviati - le navire étant remplacé par un vélo se déplaçant en ligne droite à vitesse pratiquement constante.

Un cycliste, lâchant une petite balle, est filmé à l’aide d’une caméra fixe par rapport au chemin.

Q1. Quel est le problème posé ?

Q2. Que faut-il faire pour y répondre ?

 

2.      Traitement informatique de l’enregistrement vidéo

 

Le logiciel AVIMECA permet d’étudier le mouvement uniforme d’un cycliste lâchant verticalement une balle, mouvement filmé à raison de 25 images par seconde. On peut décomposer son mouvement image par image et repérer plusieurs points d’une même image.

 

a.            Chargement du fichier

Allumer l’ordinateur puis ouvrir AVIMECA (à démarrer, programmes, Chimie Physique).

A partir du menu fichier, ouvrir la vidéo « Balle et vélo 1.avi » (à Lecteur groupes, Elèves, 207, Consulter, TP phy n°7).

 

b.            Réglages préliminaires

è Pour ajuster la taille de l’image à l’écran cliquer sur l’icône .

è Les icones situés en bas à gauche de l’écran permettent de lire la vidéo soit en une fois ou bien en mode image par image.

è Se placer sur l’image 14.

è Dans l’onglet étalonnage, sélectionner « origine et sens des axes », puis sur l’image, placer l’origine du repère (à gauche de l’image, au niveau de la partie basse de la roue)

è Dans l’onglet étalonnage, sélectionner échelle en y. Les deux points sont à placer le long du mur (entre le sol et le rebord de la fenêtre). La hauteur à indiquer est alors 2m.

è Revenir à l’onglet mesures. Le pointage sera effectué entre les images 14 et 30. Sélectionner l’image 14 comme origine des dates.

è Deux points par image seront relevés, l’indiquer dans l’écran principal

 

c.             Repérage des différents points

è Dans le tableau de mesures, sélectionner la case correspondant à la première mesure.

è Avec le curseur pointer sur : le centre de la balle puis un point du cadre (pour chaque image on sélectionnera le même point du cadre).

è Si vous vous êtes trompé, les points du tableau peuvent être effacés

è Refaire plusieurs fois cette manipulation jusqu’à l’image 30.

 

d.            Exploitation sous REGRESSI, tracé des trajectoires

è Pour exporter les points relevés sous REGRESSI cliquer sur l’icône suivant   puis sur OK.

è Ouvrir le tableur REGRESSI (à Démarrer, programmes, Chimie Physique, Regressi 2009) et cliquer sur Fichier, nouveau, presse-papiers. Les mesures sont alors copiées dans REGESSI.

è Pour tracer la trajectoire de la balle en prenant le vélo comme référence, on va créer deux nouvelles variables xREL et yREL de la manière suivante :

-          Dans l’onglet grandeurs, cliquer sur ajouter ;

-          Dans la fenêtre qui s’ouvre sélectionner « grandeur calc » ;

-          Le symbole de la grandeur est xREL, son unité est le mètre (m) et son expression est x1-x2 ;

-          Valider puis faire la même opération pour yREL.

è Pour tracer les deux trajectoires, retourner dans l’onglet Graphe et cliquer sur l’icône . Commencer par supprimer deux des courbes qui ont été créées lors du transfert des données. Décocher l’option abscisse unique. Sélectionner l’abscisse et l’ordonnée de la trajectoire de la balle par rapport au sol. Dans les options de représentation cocher ligne et point. Ensuite sélectionner l’onglet de la deuxième courbe. Sélectionner l’abscisse et l’ordonnée de la trajectoire de la balle par rapport au vélo. Dans les options de représentation cocher ligne et point.

 

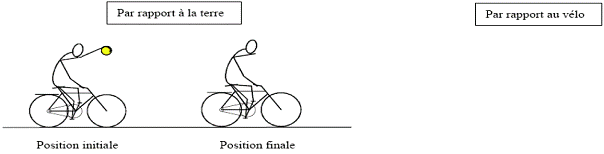
3.      Questions

Q1. D’après le fichier vidéo, où tombe la balle (par rapport à sa position de départ) ?

Q2. D’après les trajectoires obtenues à l’ordinateur, donnez un nom au mouvement de la balle par rapport à la terre ?

Q3.  De même pour le mouvement de la balle par rapport au vélo.

Q4. Représenter la trajectoire de la balle sur les schémas ci-dessous :

 

III.           CONCLUSION

Q1. Quelle réponse peut-on apporter au problème posé ?

Q2. Qui de Simplicio ou de Salviati a raison ?

Q3. Indiquer quelle est l’erreur commise par l’un des personnages ?

Q4. Par temps de brume intense, sans aucun repère extérieur, Salviati peut-il savoir si le navire est en mouvement rectiligne uniforme ou en repos ?

Q5. Cette expérience permet-elle de confirmer ou d’infirmer la phrase en gras dans le texte ?

 

IV. Quelle est la trajectoire d’un point de la roue du vélo

Sur la vidéo, faire le même travail de pointage que précédemment en sélectionnant comme premier point le repère en plastique placé dans les rayons de la roue avant du vélo et comme deuxième point le centre de la roue avant du vélo. Réaliser le pointage entre les images 10 et 31. Effacer d’abord le tableau de mesure précédent.

Tracer sous REGRESSI comme précédemment la trajectoire du point 1 par rapport au sol puis par rapport au centre de la roue. Tracer en plus la trajectoire du centre de la roue par rapport au sol.

Les reproduire ci-dessous :

Trajectoire des deux points par rapport au sol	Trajectoire du point 1 par rapport au centre de la roue.

 

V.    Nouvelle référence d’observation

Dans AVIMECA, ouvrir la vidéo intitulée « Balle et vélo 2 ». Réaliser les mêmes opérations que dans le paragraphe II.2.

Q1. Quelle est la trajectoire de la balle ?

Q2. Comment peut-on expliquer que cette trajectoire n’est pas exactement celle à laquelle on pourrait s’attendre ?

 

<<<<<< Retour

Haut de la page