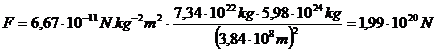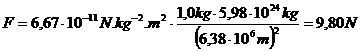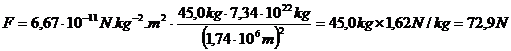Menu Lycée Collège Et Plus
|
La gravitation universelle
I. L’interaction gravitationnelle entre deux corps
è Voir poly document 1
Définition : Tous les corps qui possèdent une masse sont en interaction* gravitationnelle : ils exercent les uns sur les autres des forces d’attraction* gravitationnelle. * interaction = action réciproque entre deux objets * attraction = action d’attirer
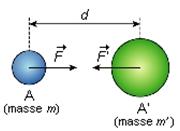
Loi de gravitation universelle : lorsque deux corps de masses m et m’ sont à répartition sphérique de masse, l’expression de la valeur des forces gravitationnelles attractives exercées par chacun des deux corps l’un sur l’autre est :
è F et F’ sont exprimées en newton (N) è M et m’ sont exprimée en kg è D est la distance entre les centres des deux corps (en mètre) è G est la constante de gravitation universelle et elle vaut 6,67.10-11 N.kg-2.m2.
Rem : corps à répartition sphérique de masse à le corps est une sphère dont la masse est répartie de manière homogène.
Représentation de la force d’interaction gravitationnelle :
Exemple : Calculer et représenter sur un schéma la force d’attraction gravitationnelle exercée par la Terre sur la Lune. Données : distance Terre-Lune : 3,84 x 105 km ; masse de la Lune : 7,34 x 1022 kg ; masse de la Terre : 5,98 x 1024 kg Corrigé :
Rem : La force exercée par la Lune sur la Terre a la même valeur.
Autre exemple : Calculer la force d’attraction gravitationnelle exercée entre deux balles de diamètre 9 cm, de masse 250 g chacune, situées à 1 cm l’une de l’autre.
Rem : La valeur de cette force est très faible et on n’en voit pas les effets.
II. La pesanteur : attraction terrestre
Exercice : (1) Sachant que le diamètre de la Terre vaut 12760 km, calculer la force d’attraction gravitationnelle exercée par la Terre sur un objet de 1 kg environ posé au sol (au niveau de la mer). (2) Même question si l’objet est situé à une altitude de 30 m. (3) Même question pour un objet de 45 kg.
Corrigé : (1) On a d = 6380 km = 6,38 x 106 m donc :
(2) On remarque que l’altitude 30 m est négligeable par rapport au rayon de la Terre. La force trouvée est donc la même qu’à la question précédente.
Conclusion : Sur Terre, à condition que l’altitude d’un objet ne soit pas trop élevée, la force d’attraction gravitationnelle exercée par la Terre sur un objet de masse m vaut : F = 9,8 × m On appelle g = 9,8 N / kg l’intensité de la pesanteur sur Terre.
Remarque : La valeur de g est légèrement différente selon le lieu où l’on se trouve sur Terre, car la Terre n’est pas exactement sphérique : elle est légèrement aplatie aux pôles (gpôles = 9,83 N / kg ; géquateur = 9,79 N / kg ; gParis = 9,81 N / kg)
Définition : Sur une planète donnée, le poids d’un objet est la force d’attraction gravitationnelle exercée par la planète sur cet objet. Cette force vaut F = m × g (g dépend de la masse et du rayon de la planète).
Exercice : (1) Un objet a pour masse 2,00 kg sur Terre. Quelle est sa masse sur la Lune ? (2) Calculer le poids d’un objet de 45,00 kg sur la Lune, le comparer au poids d’un même objet sur Terre.
(1) La masse d’un objet est la même quelque soit l’endroit considéré. La masse de l’objet est donc égale à 2,00 kg que ce soit sur Terre ou sur la Lune. (2) Sur la Lune :
Sur Terre :
III. Trajectoire d’un projectile è Voir TP de physique n°9
1. Trajectoire d’un projectile sur Terre
Dans le TP nous avons vu que lorsqu’on lance un projectile sur Terre : - Plus la vitesse initiale est grande, plus le point de chute est éloigné - Le point de chute dépend de la direction de lancement (elle est maximale pour un angle de 45° avec le sol).
Nous avons aussi remarqué que la pesanteur ne modifie que le mouvement vertical de la balle, et non son mouvement horizontal, qui reste uniforme. Quelles que soient les conditions de lancement d’un projectile, la force qui s’applique à celui-ci modifie la vitesse dans sa propre direction mais n’agit pas dans la direction perpendiculaire.
2. Mouvement de la Lune et des satellites è Voir poly document 2
Pour mettre un satellite sur orbite, il faut l’envoyer à une certaine altitude puis lui donner une vitesse initiale. Si des conditions particulières sont respectées, le Satellite va tourner autour de la Terre, il sera retenu par celle par l’intermédiaire de la force d’attraction gravitationnelle. De même, la Lune a un mouvement circulaire autour de la Terre. Elle est attirée par celle-ci mais sa vitesse permet de la maintenir en orbite.
|
||||||||