<<<<<< Retour

Télécharger :

MPI n°10 : Convertisseur décimal ÑÒ binaire

Objectifs :

• Savoir faire une conversion entre la base décimale et la base binaire
• Réaliser un outil de calcul avec Excel

I.       Rappels

Un nombre écrit en base 2 s’appelle un nombre binaire.

1.      Conversion binaire à décimal

Exemple :

On écrira alors :

(11001001010)₂ = 1 x 2¹⁰ + 1 x 2⁹ + 0 x 2⁸ + 0 x 2⁷ + 1 x 2⁶ + 0 x 2⁵ + 0 x 2⁴ + 1 x 2³ + 0 x 2² + 1 x 2¹ + 0 x 2⁰ = 1610

è  On peut généraliser cet exemple à tout nombre binaire.

@ Convertir le nombre binaire (10101)₂ en base 10 :

2.      Conversion décimal à binaire

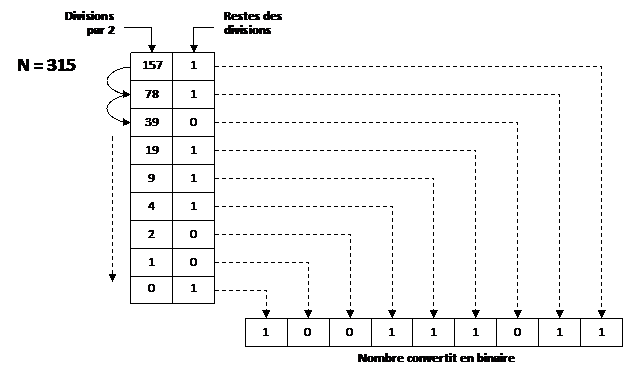
Pour convertir un nombre décimal en nombre binaire il faut décomposer le nombre en puissances de 2, pour cela, on procède par divisions successives par 2.

Exemple :

à Ainsi 315 s’écrit 100111011 en binaire.

@ Convertir le nombre 37 en binaire :

II.   Réalisation d’un convertisseur décimal ÑÒ binaire

Nous allons maintenant créer un outil de calcul Excel permettant de réaliser une conversion d’un nombre décimal entier en nombre binaire et inversement.

La figure ci-dessous montre la fenêtre principale de l’outil de calcul.

è Commencer par reproduire ce tableau sous Excel.

Attention : les cellules correspondant aux nombres en base 10 sont fusionnées alors que celles correspondant aux nombre en base 2 ne le sont pas (17 cellules comprenant soit un 0 soit un 1).

è L’objectif est de rentrer un nombre décimal (ou binaire) dans la cellule correspondante et que le résultat de la conversion s’affiche automatiquement.

è Commençons par la conversion binaire à décimale :

·         Comment convertit-on le nombre binaire du document ci-dessus en nombre décimal ?

·         Quelle formule faudra-t-il donc écrire dans la case « Conversion en nombre décimal » pour obtenir le résultat recherché ?

On rappelle que dans une cellule Excel :

-          une formule de calcul commence par le signe =,

-          on peut effectuer des calculs en utilisant la référence d’une cellule à la place d’un nombre

-          2¹⁰ s’écrit 2^10.

·        Taper la formule dans la cellule correspondante d’Excel et vérifier que la conversion fonctionne bien.

è Plus difficile !! Passons maintenant à la conversion décimale à binaire

·        Pour réaliser une division Euclidienne par 2 avec Excel, on procède de la manière suivante :

-          Pour calculer le quotient on utilise la fonction ENT qui renvoie le nombre entier inférieur le plus proche d’un nombre quelconque.

Par exemple, la formule = ENT (97,9) donne 97 ou bien = ENT (108,1) donne 108.

Donc, la formule, = ENT (315/2) me donne le quotient de la division 315/2.

-          Pour calculer le reste de la division, quel calcul doit-on réaliser ?

·        Comment réaliser alors les divisions successives pour convertir comme au paragraphe I.2 un nombre décimal en nombre binaire ?

Prenons le même exemple que dans ce paragraphe. Quelles formules doit on utiliser avec Excel ?

·        Généralisons maintenant ce résultat pour pouvoir convertir un nombre quelconque (on se contentera de convertir des nombre inférieurs à 131 072 de manière à ce que le nombre binaire tienne au maximum dans 17 cases).

-          Dans Excel, réaliser les divisions successives dans un tableau du même type que celui qui est ci-dessus. On réalisera au maximum 17 divisions.

-          Ensuite afficher la valeur des différents restes dans la case « Conversion en nombre binaire de l’outil de calcul »

·        Vérifier que le convertisseur fonctionne bien !